Ranza Research

There is no “measurement problem” in Quantum Mechanics

22Oct22

The purpose of this post is to show that there is no mystery in the measurement process from the perspective of standard quantum mechanics. It is based on my (rather vocal) comment under the recent ycombinator news story which again spreads popular, but misguided views about quantum mechanics.

The community

Many people I know seem to think about quantum mechanics as this ultimate complicated theory that is impossible to learn. This is of course in some aspects a fair statement, but not surprising given the amount of wrong things one can read about it.
Many physicists I know, just go along with it and apply it. It was even the advice given by my second quantum mechanics lecturer – which for me was the ultimate incentive for learning it deeply.
Small random (in the sense of academic achievement) subgroup of my fellow physicist, when asked in depth, agreed that doing quantum mechanics (QFT etc.) leaves them “feeling” differently than when applying the rest of the theories in physics (including General Relativity), as if there’s some missing “enjoyment” in doing quantum mechanics. I certainly agree with this point and I have some suspicions about the answer to why it is so, and no, it’s not only about its probabilistic nature, but I will leave the topic for another post.
There’s also Jarek Duda, who, like some others, sometimes older physicists, once at peace with QM, suddenly can no longer accept its truths and are looking for an alternative theory. I have respect and sentiment towards Jarek’s and other attempts, because it represents the true quest for truth, even if many of the attempts fail. Besides, he clearly deserves to be given the time to pursue his scientific itches given his outside-the-box thinking skills.
Finally, there’s one last group: The Patchers. The group is mainly composed of new-comers, but sometimes people with academic title who just got a little lost. It might have been due to the fast-paced academic curses and the general attitude of just following the maths. The existence of the older folks in the previous group, the Rejecters, and the media (even journal article headlines!) certainly accelerate the enthusiasm of newcomers – who, unequipped with enough understanding of the existing framework to build something entirely new, try to patch places which not only do not require patching – the patches won’t “stick to it” even in principle.

Not surprisingly, many of them skims through the fundamentals and goes straight to the Schrödinger Cat like paradox. After all, that’s the ultimate thought experiment that tries to reconcile the quantum framework with macroscopic observations. And no, naming it “the measurement problem” doesn’t make any difference. It’s still the same old “insight” as it was in 1930.

In what follows, I’ll try to present how standard quantum mechanics gets out of the Schrödinger Cat paradox and convince you that just supplementing or patching the Born rule isn’t an option. I will not consider interpretations of quantum mechanics as they do not bring much to the table for a physicist. I personally believe that the reasons quantum mechanics is the way it is can and will be found, but an interpretation is just a shoot in the dark. There’s no way to verify it.

The gist

The reasoning below comes from John von Neumann and from Wojciech Żurek. I’m fairly certain that von Neumann was aware of the details even if he didn’t spell out all of them.

To get the argument across, let’s assume that $\psi$ describing our particle is a superposition of two eigenstates:
$|\psi \rangle = c_1 |1 \rangle + c_2 |2\rangle$ , where $|c_1|^2 + |c_2|^2 = 1$ .
Without loss of generality we can pick:
$c_1 = x$ and $c_2 = \sqrt{1-x^2}e^{i \phi}$ , where $x <1$ is a real number.
The density matrix of this pure state can then be written as $\rho = |\psi \rangle \langle \psi|$ and
one by writing the explicit form of this density matrix one can see that the diagonal terms are:
$x^2$ and $1-x^2$ , while the non-diagonal terms are:
$x \sqrt{1-x^2} e^{i \phi}$ and $x \sqrt{1-x^2} e^{-i \phi}$ .

In the most complete scenario of a measurement, the density matrix of the system can change in many ways, including the diagonal terms of the density matrix. However, in this simplistic example, a measurement will, from construction, bring only the non-diagonal terms to zero (I hope most of the interested readers will have enough background to understand why).

Now, the measuring device, as a macroscopic object, will have the number of degrees of freedom far greater than the simple particle of which state we’re about to measure. This number will be the order of the Avogadro number (~ 10^23) – even the smallest human visible indicator will be this big. The measurement, by necessity, includes an interaction of our small system with the enormous measuring device.

Before the interaction, the whole system (the particle and the measuring device) can be written as a tensor product of the two wave-functions:

$|\Omega_{before}\rangle = |\psi\rangle \otimes |\xi\rangle = ( c_1 |1\rangle + c_2 |2\rangle ) \otimes |\xi\rangle$

where $|\xi\rangle$ represents the wave-function of the measuring device and everything it interacts with before the measurement. When the interaction occurs the state of our measuring device changes unitarily (as everything in nature) according to the full Hamiltonian of the system, and with some regrouping of the terms, we can write the state after the interaction as:

$|\Omega_{after}\rangle = c_1 |1\rangle \otimes |\xi_1\rangle + c_2 |2\rangle \otimes |\xi_2\rangle$

This is the true state of the system as unitarily evolved by nature.
The individual subsystems are no longer in pure states, but the whole system $|\Omega_{after} \rangle$ (even if we’re unable to completely describe it) – is.

Now, comes the final part, which some call the “collapse”, but in reality it is just “an average” over all possible states of the bigger (measurement) system which we declared a priori not be our system of interest and states of which we are not able to follow because we measure with it:

${Tr}_{\text{device's degrees of freedom }} |\Omega_{after}\rangle \langle \Omega_{after}|$

In result, we obtain a reduced matrix with only diagonal elements $x^2$ and $1-x^2$ , containing “classical” information about the possible results of measurements. We could use this information to again resume our experiment from a “classical checkpoint”. Note that we have just lost the off-diagonal terms, in this case phases.

Why are off-diagonal terms zero?
Let’s inspect one of the non-diagonal terms over which the above trace is taken:
$x*\sqrt{1-x^2} e^{i \phi}$

It is effectively zero, because the trace over the degrees of freedom of the measuring device is a multiple integral, again of the multiplicity of order of Avogadro’s number and a similar number functions which change in various ways. It is enough that only a fraction of such integrals will have a value lesser than 1 to guarantee that the product will be equal to a practical zero.

And this is all. I hope that it now becomes clear that the measurement procedure has a well-established place in quantum mechanics and is built on top of previous assumptions about its probabilistic nature. The very unfamiliar features (to a classical mind) of quantum mechanics occur at the very start, where we are made to accept superpositions: not when we convert the information to the macro environment. Hence, any attempt to change “patch” or “reformulate” the measuring process would need to reject quantum mechanics completely, because probability calculus is at the very heart of it.

Bonus aid #1

Simple truths about quantum mechanics:

1) The wave-function is only the DESCRIPTION of the underlying phenomena.
2) Within this description, everything, and I mean everything, evolves unitarily. No exceptions ever.
3) Whenever you decide to measure, i.e., probe the microscopic system with an object that is not within your quantum description, i.e., have no details about all the phase/amplitude information you’re destined to average/trace over the unknown states (apply the born rule), as was done above. That’s always what we’re left with in case of a large system outside of our description interacting with a small system within our description.

On the other hand, if you put a small quantum system, with another small quantum system (say two particles), there’s no need to trace/average/apply the born rule immediately because your description can be complete both in principle and in practice: you can just unitarily evolve the system for as long as you wish/can compute for.

However, sooner or later you’ll want to measure, because ultimately that’s what physics is all about – verifying your predictions with experiment – and you go back again to small vs big, because that’s the only way we, humans, can perceive the microscopic reality. The result will be completely analogous to the one before, the only change being that you’ll now be able to predict probabilities of a two-particle system.

Do you feel uneasy with QM wave-functions which have the status of descriptions of reality?
Go and study classical field theory in which the fields are to be thought of as real physical entities.
go step deeper and you’re in quantum field theory in which you deal with descriptions again.
Would a theory in which we deal with “real physical entities” be better than that of “descriptions”?

Bonus aid #2

There are some parallels between electrodynamics and QM that might help a little in making QM less unfamiliar.

One example is that you can have your complete description with the four-potential, about which you know, from the Aharonov-Bohm effect, carries more information than electric/magnetic fields alone, although fields are the only thing we measure – not the electric/magnetic potentials. The potentials were the side product of the formalism that turned out to have real consequences. In a similar matter, we learned the importance of the wave-function/phases in the description, even though we only measure probabilities.

Filed under: Physics, Science | Leave a Comment
Tags: measurement, mechanics, quantum

Never forget things once learned

18Sep15

This was the challenge I’ve set out before myself, which lead me to creating MathematicaAnki tools (picture below).

Note taking with Mathematica and review of notes in Anki

“My final suggestion is to pick some sort of organisational system and make a real effort to stick to it; a half-hearted system is probably worse than no system at all.”

Terence Tao

There’s an enormous amount of things I don’t know, even larger things I don’t know that I don’t know – but that’s the good news.

The bad news is that I’m forgetting stuff in an incredible pace – well, of course I’m quite happy forgetting all the workarounds around broken things on Windows (now that I work on OSX), what scares me though is the amount of maths and science in general I’ve forgotten over the years.

There are two ways of fixing it:

Learn things deeply, make a lot of exercises, use the knowledge extensively.
Organize your knowledge and recall it from time to time.

Of course the best way is to use both techniques all the time, but only the second way can be improved with technology (prove me wrong in comments).

Now you don’t want to use bad technology which can only work half of the way and discourage you – as prof. Tao pointed out. Equations and pictures are the things I can’t live without so I needed something which can do both, not just text; typing equations should be simple and fast. I wanted something that will work on my laptop as I don’t consider my phone a good tool for typing. Moreover if I’d be able to do some calculations in the same place that would make it beyond awesome. So I’ve picked Mathematica (bare LaTeX wouldn’t be such a bad choice, but I have a free license from University) and combined it with Anki – a flash card app. My aim was to write things once and then highlight the things that are difficult and create flashcards from them. Flashcard not only text, but also equations and pictures. I’m really excited with the result and happy to finally share it with you. If you’re interested you can find it here on my GitHub profile.

Don’t let the new academic year catch you by surprise!

Filed under: Science | Leave a Comment
Tags: anki, intelligence, learning, math, note, Tao, Terence Tao

Density of states in nanostructures

19May15

Some notes from my classes and worth seeing (if not remembering) results.

We’d like to calculate the function $D(E)$ called density of states, for systems with partially restricted dimensions. In fact all of the considered cases are 3D, they’re just confined spatially in one (2D) or two directions (1D).

Starting from the general term for density of states

$D(E)=\sum _{\mu } \delta \left(E-E_{\mu }\right)$

where $\mu$ is the collection of all quantum numbers, we can calculate the terms for density of states for 3D, 2D and 1D cases.

3D case

In the 3D case we don’t have any restrictions, therefore changing the sums over $\mu$ to integrals over all possible states enumerated by $k$ vector we get:

$D(E)= 2 \frac{V}{(2\pi )^3} \underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }} \delta \left(E-\frac{\hbar ^2}{2m}\left(k_x^2+k_y^2+k_z^2\right)\right)dk_xdk_ydk_z$

Where the term $\frac{V}{ (2 \pi )^3 }$ is the phase space occupied by a single state and the integer $2$ comes from two possible spins for each state.

$D(E)=2 \frac{V}{(2\pi )^3}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{\pi }{\int }}\underset{0}{\overset{\infty }{\int }}\delta \left(E-\frac{\hbar^2k^2}{2m}\right)k^2dk \sin \theta d\theta d\varphi =$
$2\frac{V}{(2\pi )^3}4\pi \underset{0}{\overset{\infty }{\int }}\delta \left(E-\frac{\hbar ^2k^2}{2m}\right)k^2dk= \begin{vmatrix}{c} \frac{2m E_{\zeta }}{\hbar ^2}=k^2 \\ \frac{1}{2}\frac{\sqrt{2m} }{\hbar }\frac{dE_{\zeta }}{\sqrt{E_{\zeta }}}= dk \end{vmatrix} =$
$2\frac{V}{(2\pi )^3}4\pi \frac{1}{2}\frac{\sqrt{2m} }{\hbar }\frac{2m}{\hbar ^2}\underset{0}{\overset{\infty }{\int }}\sqrt{ E_{\zeta }}\delta \left(E-\sqrt{E_{\zeta }}\right)dE_{\zeta }=\frac{V}{2\pi ^2}\frac{(2m)^{3/2}}{\hbar ^3}\sqrt{E}$

2D case

In 2D case the values $E_z^n$ are enumerated by integer $n$ , therefore we don’t convert one of the sums.

$D(E) =2 \frac{S}{(2\pi )^2}\sum _n \underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}\delta \left(E-\frac{\hbar ^2}{2m}\left(k_x^2+k_y^2\right)-E_z^n\right)dk_xdk_y=$
$2\frac{S}{(2\pi )^2}2\pi \sum _n \underset{0}{\overset{\infty }{\int }}\delta \left(E-\frac{\hbar ^2k^2}{2m}-E_z^n\right)kdk= \begin{vmatrix}{c} \frac{\hbar ^2}{m}kdk=dE' \\ k dk = \frac{m}{\hbar ^2}dE' \\ \end{vmatrix}$

$\frac{S}{\pi }\frac{m}{\hbar ^2}\sum _n \underset{0}{\overset{\infty }{\int }}\delta \left(E-E_n-E'\right)dE'=\frac{S}{\pi }\frac{m}{\hbar ^2}\sum _n \theta \left(E-E_n\right)$

1D case

In 1D case the values $E_z^n$ $E_y^m$ are enumerated by integers $n$ and $m$ , therefore we don’t convert two of three sums.

$D(E)= 2 \frac{L}{2\pi }\sum _n \sum _m \underset{-\infty }{\overset{\infty }{\int }}\delta \left(E-\frac{\hbar ^2}{2m}k_x^2-E_z^n-E_y^m\right)dk_x=$
$\frac{L}{\pi }\sum _n \sum _m \underset{-\infty }{\overset{\infty }{\int }}\delta \left(E-\frac{\hbar ^2}{2m}k_x^2-E_z^n-E_y^m\right)dk_x= \begin{vmatrix}{c} \frac{\hbar ^2}{m}kdk=dE' \\ dk = \frac{m}{\hbar }\frac{dE'}{\sqrt{2m E'}} \\ \end{vmatrix}=$
$\frac{L}{\pi }\frac{m}{\hbar }\frac{2}{\sqrt{2m}}\sum _n \sum _m \underset{0 }{\overset{\infty }{\int }}\delta \left(E-E_z^n-E_y^m-E'\right)\frac{1}{\sqrt{E'}}dE'=$
$\frac{L}{\pi \hbar }\sqrt{2 m}\sum _n \sum _m \frac{1}{\sqrt{E-E_z^n-E_y^m}}\theta \left(E-E_z^n-E_y^m\right)$

Filed under: Notes, Physics, Science | Leave a Comment
Tags: density, nanostructures, Physics, quantum, science

[Updated] Fix Mavericks slow Quick Look in Finder

01Nov13

Turns out Apple didn’t mess it up.

The real reason is SMB file sharing. Just go to System Preferences -> Sharing -> Options… and disable Share files and folders using SMB and you’ll notice immediate boost in responsiveness! via http://forums.macrumors.com/showthread.php?t=1662449&page=3

Filed under: Fix, Tweaks | 5 Comments
Tags: Apple, fix, improvement, Mavericks, osx, Preview, Quick Look, Slow

OSX Productivity Tip NO.1

16Jun13

I’ve thought that I was done writing this kind of stuff, but I’m about to tell you something amazingly simple and yet very cool.

Just go to:

System Preferences -> Keyboard -> Keyboard Shortcuts -> Services – that’s it.

There’s a hell lot awesome stuff you can do here.

Just remember to pick up a key modifier that would not interact with other apps. Command + Control is quite a good choice.

Here’s a bunch of cool stuff that I did:

1. Open an address in Google Maps [ ^ ⌘ G ]

Open address

This is minor but possibly time saving.

2. Import image [ ^ ⌘ O ]

This is really useful – importing photos from iPhone straight to a document/note

Screen Shot 2013-06-16 at 15.28.19

3. Capture selection from screen [ ^ ⌘ P ]

Complementary to the previous tip – you can capture part of the screen directly.

4. Send to Kindle [ ^ ⌘ K ]

I often choose to read things on Kindle instead of a lcd screen, this tip just reduces the number of clicks between Kindle and my laptop. Note: You need Send to Kindle app installed in order to use it.

5. Upload with CloudApp [ ^ ⌘ U ]

Instead of dragging why not just use a keyboard shortcut? Note. You need Cloud App .

6. Look Up in Dictionary [ ^ ⌘ D ]

This is actually cooler than I thought. You can translate stuff just by putting the cursor over them, even in system windows!

7. Unarchive To Current Folder [ ^ ⌘ Z ]

Major relief from clicking.

8. Typeset LaTeX Maths Inline [ ^ ⌘ M ]

I’ve left the coolest for the end – this let’s you change a LaTeX text into a nicely rendered picture in apps like Evernote – very useful for making science notes. Note. You need to download LaTeXian and change it’s default format from PDF to PNG.

And that’s just what I’ve discovered, what will you come up with?

Filed under: Blog Technical, Personal, Tips | 38 Comments
Tags: alfred, Apple, evernote, keyboard, Keyboard shortcut, latex, mac, Mac OS X, osx, productivity, System Preferences, Utilities

Memory, mathematics and synesthesia.

02Jun12

Sometime ago I saw a TedTalk done by Mr. Daniel Wolpert, which now (once I’ve watched it again) made an even deeper impression on me; The bayesian predictions and the feedback loops are surely something worth thinking about, but the first time I’ve watched it I’ve became instantly occupied with one of the very first sentences he said, paraphrasing: “The brain exists in the first place to produce motions.” (1)

This thought surely stirred a lot of thinking in me and at first I wasn’t in perfect agreement with it either, but gradually over time I’ve become accustomed to this thought and now I can point a lot of other clues that happen to fit well with it.

Let me give you one example – Recently on TED I saw another TedTalk (which I can’t get a direct link to) in which Mr. Joshua Foer talks about his research on developing amazing memory. He postulates convincingly that our memory capabilities can be extended using our imagination. He even goes on to present some evidence, in which they’ve put both; normal people and the memory savants into an fMRI machine while in the process of remembering and it turns out that the only difference between them was that the memory savants tended to use their spatial memory and navigation areas of the brain… Ehm, sorry, what did you say again? Correct, spatial and navigational areas of the brain. It turns out that we have an exceptional spatial memory. Mr. Foer goes on bringing up ancient orators using the spatial technique and old linguistic analogies to places. The question he asked himself was whether he could perform the same after some training – the answer turned out to be ‘yes’. We can train our minds to pay attention and remember, by recalling the ancient strategies that seem to be forgotten in the era of quick internet access, remainders and flash memory drives.

You may ask what are those strategies precisely doing – are they creating abstract worlds in which we can perform our imaginary walks? It seems so, and in the context of (1) it seems that our brains are just building upon what’s already there, borrowing the method. In other words we’re just looking at the work of the good old patchy-evolution, which tends to translate facts into something the navigating brain can understand and move between – space of events.

Now I’d like to tell you about something that lately occurred to me. This hypothesis may not turn out entirely new ( or true : ) ), but a discussion in the comments would be very welcome.

What if our effectiveness at Mathematics depends on similar strategies, which tend to make our ways of thinking a little more synesthetic?

Mathematics is a universe. Mathematicians are the pioniers, the explorers of new and unknown before. Then, eventually, the paths become so common that they become widely known by many.

One may now think: Wouldn’t it be wonderful if we could come up with a mathematical proof, simply by thinking about a way of getting to a specific point in space? An analogy of saying ‘go straight, then turn right, climb the stairs’…

In the first part of this article we’ve been talking about remembering things that didn’t necessarily have any predefined relation to each other. Mr. Foer taught us how to remember things by using made up connections to create a palace over which we could walk through the eyes of our imagination and amuse ourselves.

Mathematics doesn’t give us that much freedom, it constrains us, in similar fashion that the reality does. While the memory palaces created on Memory Contests are goofy and arbitrary, the palaces of Mathematics need to be ones of fine structure, not connected in arbitrary fashion. Therefore Mathematics is about discovering bridges between islands and describing their properties (is it a one way bridge? does the bridge lead to a parent island or to child island) instead of creating them. Sometimes you even have to stop and decide whether you’ve landed on the same island or a new one.

Of course making up a connection is easier than actually finding out what the connection is, but hey – that’s Math, an activity for real man. How could we get better at it? This was a question I’ve asked myself and I came up with a few proposals:

Think about the types of possible connections between structures and compare them with the ones defined already in math (injection, surjection, morphisms etc.)
Try to get a good mental picture of each of them, try to associate a color/smell/feeling with each one. Perhaps the relations relate somehow to each other – try to take that into account too.
Train logic interference – that is, the speed and accuracy of the evaluation of logic statements (I’m planning to create an app for this during the weekend, but in meantime you can take a look on this cambridge test which provides one test similar to what I’m about to implement)
Translate mathematical objects into space events and use the relations to connect them together building a Math Palace, then take a hike around the place.

In case of memory, Mr. Foer showed us that we can build highways in places where fragile country roads had been. I don’t know how far we can stretch that intuition, but nevertheless I found it worthwhile to think about.

Here’s a bonus thought: Doing Physics requires somehow an inverse process.

It’s process of finding the right structures from the mathematical universe and trying to fit them to the structures of the real world.

Feel free to argue with me in the comments below.

[Edit: 6 May 2012 16:32]

While planning the inner workings of the new app I’ve started researching the topic on pubmed and found some research that seem to back up my hypothesis:

“Results suggest that spatial abilities and language comprehension, but not basic numerical processing, may play an important role in advanced mathematics.”

“…results of the present study imply that the neural substrate, which is potentially necessary to enhance specific skills dramatically by positively motivated excessive mental training, might be present in every healthy individual.”

[Edit: 9 May 2012 13:48]

I’ve just finished reading Joshua Foer’s book ‘Moonwalking with Einstein’ and I must say that while I had moments of feeling towards discarding this book as completely invaluable, it would be unreasonable to do so.

However, I should warn everyone that saw his TedTalk that he doesn’t in fact use the memory techniques that he so much promoted on the TedTalk, instead in his book he just promotes mindfulness.

His book doesn’t contain any kind of special recipe for improving everyday memory, instead it leaves open questions, describes the history of memory improvement, savants, the process of mastering a skill (worth reading) and his own experience at the memory contest.

That story leaves yet another doubt to how much we can improve ourselves and to the validity of my hypothesis.

Filed under: Memory, Neuroscience, Science | 5 Comments
Tags: brain, consiousness, daniel wolpert, hypothesis, ideas, memory, neuroscience, science, talks, ted

Xcode 4.3.2 permissions [Bug]

21Apr12

I don’t know how much this was my fault, but it took me some time to figure this out.

Problem:

Anyway Xcode couldn’t access my iPhone 4, nor another iPhone 4 nor iPad 2. The error that I keep getting in the Organizer was:

Xcode has encountered an unexpected error (0xC00D)Permission denied, at ‘/SourceCache/DTDeviceKit/DTDeviceKit-1196/DTDeviceKit/DTDeviceKit_Utilities.m:854’

I’ve tried restarting the devices, mac and reinstalling Xcode two times from the App Store. I’ve found all the internet solutions ineffective.

Solution:

I’ve found that ~/Library/Developer permissions were wrong.

Simple sudo chmod -R 777 ~/Library/Developer/ did the trick.

Filed under: Programming, Xcode | Leave a Comment
Tags: 0xC00D, bug, connect, DTDeviceKit, iphone, linkedin, organizer, permission, xcode

Systematic for iOS

14Mar12

The following quote captures the essence of Aristotle’s philosophy and uncovers a lot of motivation behind my new iOS app called Systematic.

However the real source of motivation to create this app has been my year long stay in Valencia (Spain), where more then ever before have I learned about the benefits of a well balanced life.

Not only did the balance get me more productive, but it also got me much more relaxed.

However getting to this wonderful point of balance took my about 3/4 of a year in Spain. So I’ve begin to wonder how could I speed up the whole process. How do I free myself from procrastination? Perhaps with some kind of system that would help keeping life well balanced?

Could one of the old systems be used to get to a more balanced life?

Calendars?

No, calendars are too rigid for this new purpose.
Calendars are useful for things that you must do, at a certain hour like work, lectures or meetings.

Reminders?

No, reminders need constant attention and are annoying if not set to the right hour.
Reminders are useful for things that you need to remember.

Todo lists?

No, todo lists do not repeat the task over periods of time.
Todo lists are good for keeping a list of task connected with a certain project.

So I’ve needed to develop my own application.

An app that would keep track of the tasks that you want to do repeatedly and suggest them at the right moment.

I’m really glad with how the app turned out as it’s extremely helpful for me for a bunch of reasons:

I don’t get overwhelmed by the number of tasks I need to accomplish.
It doesn’t tell me “Do X now”, it tells me “Hey, here’s a bunch of things you could be doing right now ordered by the ones most neglected”.
I don’t need to keep track of all the things in my head.
I know that even if I don’t get everything done perfectly, after some time I’ll get more efficient and do things better.

Although I already have a roadmap till version 1.1, I’m open for suggestions!

Tell me what functionality in your opinion is missing or what you’d change.

Enjoy a better life with Systematic. 🙂

Filed under: Systematic | 13 Comments
Tags: aristotle, habbit, hobby, iOS, iphone, management, motivation, pro, Systematic, time, work

Voxel visualization of brain hematoma [CT]

24Jan10

The 3rd semester of Computer Science on Wroclaw University of Technology brought to me an occasion to do something that was written for a long time in my Idealist.

After writing a 3d engine with Gouraud shading and per vertex Phong lightning model, which was the basis of evaluation of the graphics course, I’ve decided to do something more.

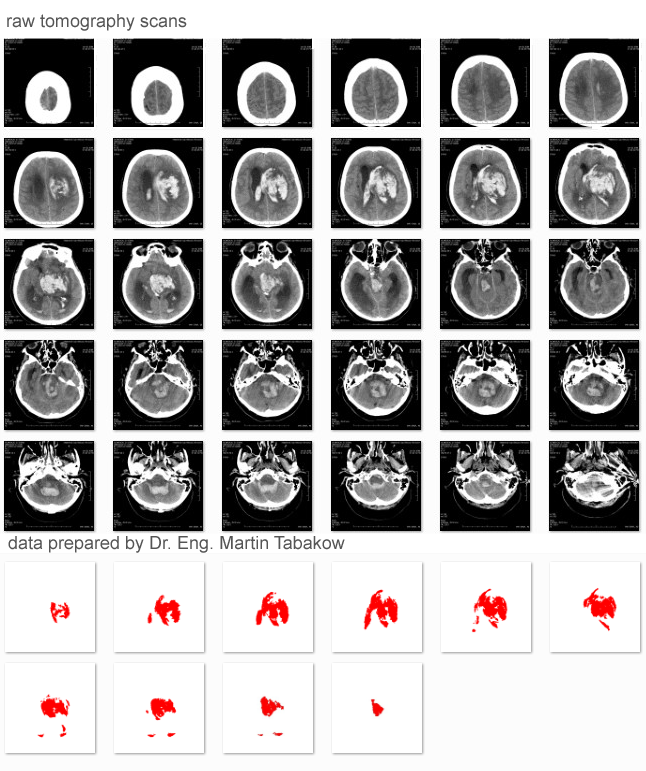
The topic was influenced by Dr. Eng. Martin Tabakow, who proposed visualizing volume information using 2D tomography scans data, segmented previously using his own algorithm.

I’ve been thinking a lot about how it could be done effectively, considering such ideas such as vertex representation using spline interpolation or adaptive surface tessellation, but after some searching and long discussions with Rychu (who is also my best personal debugger and saved me a lot of hours 🙂 ) I’ve decided to use Voxels with ray-casting as display method. After getting the basic version to work properly, I’ve added trilinear interpolation, per voxel shading and deeper raycasting (a bit slower) for getting the looks closer to those from marching cubes.

So at the end, the application takes a the segmented data, analysis it, makes interpolation in between and at the end, calulates normals accordingly to the neighboring voxels and light using Lambertian light model with attenuation. At display I’m using Smith’s cube intersection algorithm to determine the intersection points of the ray with the volume data. Then I interpolate from one point to another searching for the first non-null element and display it.

Here is the example input data:

And here are some sample results:

The application allows to move it freely and to switch from one mode to another, yet there are some things that I’d like to improve in future like a better interpolation shape and smoother edges, but maybe after some recovery from the ‘Java experience’.

Filed under: Informatics, Programming, Science, Visualization | 4 Comments
Tags: computer, CT, tomography, visualisation, Voxel

Lightmapping Tool for Maya and Mac [alpha]

18Jan10

Today I announce the first alpha version of External Lightmapping Tool that works not only with 3dsmax and Windows, but now also with Maya and Mac OSX.

So far the system was tested on Windows 7 and Mac OSX Snow Leopard with Maya 2010. The package can be downloaded from here:

http://unitylightmapper.googlecode.com/files/elt_maya.zip

How to use it?

1. Run a Unity project on which you’d like to use it, then open elt_maya.unitypackage

2. Open External Lightmapping Tool window (menu Window in Unity)

3. Point where the Maya application is installed and add objects to lightmap list and some lights to unity scene

4. Export scene (Maya should open)

More info how to use it can be found here: https://masteranza.wordpress.com/unity/lightmapping/

The system works, but I’m not a Mac user neither Maya user, so I would like to hear suggestions from you, especially when it comes to render quality in Maya using BakeSets.

I would like to make it produce as high quality renderers as it can without tedious user preconfiguration.

Filed under: Projects, Vray-Unity tools | 3 Comments
Tags: lightmapping, mac, maya, osx, quick, snow, tool, Unity, uv

Unity External Lightmapping Tool NO.4 – results

06Sep09

It’s been a while since the first post about the lightmapping tool (even the name evolved to a more general one ;)) and I handed out the system to Unity a week ago. Now the mentors are making from it a neat package and adding some example assets and I myself am making the documentation better and trying some weird stuff to make the system working even better.

I don’t want to make a false start so I won’t post the final Unity package till it’s not on their website but I’ll share a lightmapping example with you that with probably be in the system documentation.

The scene before lightmapping

Using the tool you can prepare lightmap texture atlases in Unity, simply by dragging the objects to the chosen lightmap.

Once you’ve chosen your objects press “Export Scene” button

The scene gets exported to 3dsmax (also with Unity lights), where waits for you the External Lightmapping Tool helper.

After you adjust the scene lightning in 3dsmax, this little tool will render and save the lightmap textures to your Unity project directory and apply the lightmaps automatically.

In 3dsmax you can use regular “CTRL+S” shortcut to save your materials and lightning for future changes

After the rendering is complete you can come back to Unity and see the results.

Whenever you’ll have to rebake your scene (objects or lights in scene moved), just press the “Export scene” button again.

The tool will reload the scene in 3dsmax at the point you’ve leaved it at last save.

Filed under: Projects, Unity, Vray-Unity tools | 5 Comments
Tags: lightmapping, mental ray, tool, Unity, vray

Tweak NO. 4 : Windows 7 and XP dual boot on Dell XPS M1530

04Sep09

win7xp copy

It’s some time since my post about Fedora & Vista dual boot using the Dell Media Direct button and I’ve realized that I don’t use linux at all.

It’s not that I don’t like to – I would love to switch to another more customizable system, but I can’t. Windows binded me with too many applications, 3dsmax, visual studio, Unity- just to name a few and it’s enough to make me stay.

It’s not that hard to setup this dual boot, but one false step can lead you to broking the Master Boot Record and data loss. This guide should protect you from such mistakes, however I still do not take any responsibility for the damage that can possibly be done 😛

1. Get needed tools.

Dell Media Direct CD
MBRWiz http://mbrwizard.com/index.php
GParted http://gparted.sourceforge.net/download.php [you’ll probably don’t really need this tool since in most cases you can calculate the drive index from the data given by MBRWiz, however if you want to get really sure then download it and burn to a cd]

2. Get rid of the media direct partition (not really needed, but why to keep it? 🙂 )

3. Partition your HDD in some wise way, like: partition1 – Windows XP , partition2 – Windows 7, partition 3 (extended) – data

4. Install Windows 7 to the desired partition

5. Run MBRWiz, hide the Windows 7 partition and make the Windows XP partition active, look here for examples how to do that: http://mbrwizard.com/examples.php

6. Install Windows XP to the desired (active) partition

7. Unhide Windows 7 partition

8. If you’ve downloaded GParted then run it and note the partition indexes of Windows 7 and XP (numbers shown after …\sda). If you didn’t download it and you’d like to use a trick then probably you’ll get it working by adding 1 to the indexes shown by MBRWiz – note them somewhere

9. Insert the Dell Media Direct CD, while being on Windows XP and using command line navigate to your CD drive and write: rmbr DELL X Y where X is the index to the system partition which you’d like to run when pressing the regular power button and Y is the index to the system partition which you’d like to run when pressing the Media Direct button

That’s all, enjoy your dual boot dell laptop.

There’s also a way to sync the application data between those two systems so you don’t have to install the applications twice, but I’ll either refer to my friend article when he’ll write it or write it myself someday.

Filed under: Dell XPS M1530, Tips, Tweaks | 12 Comments
Tags: 7, boot, dell, dual, m1530, setup, tweak, windows, xp, xps

Developing Unity Lightmapping tools NO. 3 : Week summary

14Aug09

I’ve changed a little bit the list for last week

Last week:

Automatic setting the lightmaps accordingly to their name as soon as they appear in Asset folder
Basic batch render script for 3dsmax, which opens max and renders&saves all lightmaps (yet hardcoded)
A solution for applying materials, and setting up lightning have been overdiscussed
An option for changing shader to lightmap-enabled one was implemented in the object list
Handling objects that are not ready for baking (non-valid uv2 map)
Lot of bugs have been repaired and code was send to the mentor for a review

render

(The Unity light is turned off :P)

scene

Some first results – scene was setup in Unity and exported using my tools to 3dsmax where it was baked

Next week:

Implement an option for exporting default Unity lights
Research, for an optimal, most universal and non-roadblocking solution for loading preset lightning and other settings to an external app which will be doing the rendering (thinking about further development)
Implementing some of the advanced options
Developing batch render script for 3dsmax
Development of some small tools for helping users which uv2 seems not to be perfect correct (scale or offset)
Code optimization, bug removal and probable reorganisation (depanding on Lucas review)

Filed under: 3dsmax, Unity, Vray-Unity tools | Leave a Comment

Developing Unity Lightmapping tools NO. 2 : Week summary

09Aug09

THIS WEEK SUMMARY:

The main core with GUI has been done which contain a following options:
A dynamic list of lightmaps (shown as buttons)
Simply hierarchy display list for currently highlighted lightmap
Most necessary options “Pick selected objects”, “Clear list”, “Export FBX”
Optimal UV Packing:
the size of lightmap spot for an object depands on its surface area
the algorithm additionally “removes empty spaces” from each UV map in packing procedure
The algorithm repeats itself with smaller sizes if packing the objects on the given lightmap area failed
ASCII FBX Exporter (working mesh, material and uv export – with a small smoothing issue)
Tested the exported fbx files in 3dsmax and Modo

FOR THE NEXT WEEK:

Automatic setting the lightmaps accordingly to their name as soon as they appear in Asset folder
Batch render script for 3dsmax
Exporting with scene preconfiguration for 3dsmax
An efficient solution for applying materials in 3dsmax
Some tools for intelligent batch shader switch on the objects which will be lightmapped, but currently don’t have a lightmap-enabled shader
Finding and eliminating current bugs

Filed under: Unity | 1 Comment

Developing Unity Lightmapping tools NO. 1 : FBX Exporter

27Jul09

After some consideration I decided to change the name for a moment to make it less confusing for other people, because the project indeed is focused on the connection between Unity and Vray over 3dsmax, but the main core will allow everybody to use it for their own purpose with any software with a FBX importer and rendering system supporting UV’s on channel 3.

After a few days of work I’ve written the main core of the FBX Exporter which now allows to export any mesh objects, with their textures and for the moment – a UV on channel 1.

At first I was a little feeling a little uncomfortable when I’ve discovered that Unity splits vertices’s, however for my current project it wasn’t such a big deal. Accordingly to the assumptions the scene should be ready for baking on the export time, so I don’t have to really think about all those additional vertices’s that will show up in 3dsmax until it looks properly.

Later I’ve been a bit impressed in how sophisticated way was the Unity API designed – it really makes writing for it easy and comfortable and that’s something I would not say about Autodesk FBX documentation, because there’s no documentation at all and the most of my time I spent on endless experiments, trying to figure how things work there inside. I still cannot say that I figure out everything cause I’m having a little smoothing problems and I didn’t test it with other objects that won’t be attached as one mesh.

At the moment I would like to give a few tips to anybody straggling with FBX in ASCII mode.

At exporting UV’s from Unity to FBX be set the “MappingInformationType” to “ByVertice” and “ReferenceInformationType” to “Direct”
Most of the properties supported by the object in an FBX file aren’t needed when you want just import it to 3dsmax, just be sure to left 6-7 last properties
When exporting a reference to a texture there’s no need to export Video objects connected with them.
3dsmax importer is tolerable when it comes to file paths, you may use “/” as well as “\”

I’ve also researched other areas like UV packing in Unity, running from command line and lightmapping in 3dsmax.

As it turn’s out, one can get a really fantastic results will well adjusted materials.

Below you can see a simple scene without any Unity light (not well unwrapped though) which shows the difference between lightmaps rendered with objects that contained bumpmaps in their materials and those which don’t.
On the bumpmaped I’ve added a little reflection to the floor and as you can see it became rendered pretty well too.
adjusted

Filed under: Unity, Vray-Unity tools | 4 Comments
Tags: lightmapping, project, tool, Unity, vray

Project NO. 3 : Unity Lightmapping tools (using Vray etc.)

21Jul09

Yesterday I’ve received an information that my proposal (+ video) which I sent for Unity Summer of Code contest was accepted and I’m really excited about the system development 🙂

Basically the system is automating the bake process for Unity powered games using a powerful rendering software VRay.

The Unity team proposed a bit different workflow and not all the original ideas will be implemented as the part of the system. It was rather clear that it would happen since the ideas I described were indeed invented rather quick for a game which I’m working on with my team (no further details now 😛 )

Nevertheless I’m very happy with the changes proposed by Unity team and those which came after the talk with my mentor Lucas Meijer. I think that it’ll all make the lightmapping process in Unity really simple and effective.

I didn’t setup my goals yet, since I want to be rather sure what exactly can be done in those 6 development weeks, but since many of you may be interested in the details I will often blog here information about the development progress and plans – starting from today. Feel free to submit here your ideas in a form of comment 🙂

Here’s the scratch of the workflow made by Joachim Ante:

From the end-users artwork we simply require:

* At import time per object unique uv’s are required (normalized to a range of 0 … 1)

[As a first step, we can just require the user to provide it, or we could automatically generate them later on]

The lightmapping process works in 5 steps:

1) Go through the scene and pack rectangle UV coordinates into a texture sheet

They can be stored in the renderer using lightmap tiling and offset: http://unity3d.com/support/documentation/ScriptReference/Renderer-lightmapTilingOffset.html

2) Create an FBX file from Unity scene. Export both the primary and secondary uv set with the packed UV coordinates.

This means that we “offset-scale pack” the per object uv’s we have, into a new “baked uv sheet”. (FBX supports Ascii mode, so it’s quite easy to export)

3) Launch Max from inside Unity through the commandline batchmode interface, automatically open the exported FBX file and start the lightmapping process

4) Once the batchmode completes, Unity imports the textures and applies them to the renderers using the Lightmap Settings class and renderer.lightmapIndex.

From the end-users artwork we simply require:

* At import time per object unique uv’s are required (normalized to a range of 0 … 1)

[As a first step, we can just require the user to provide it, or we could automatically generate them later on]

The lightmapping process works in 4 steps:

Go through the scene and pack rectangle UV coordinates into a texture sheet. They can be stored in the renderer using lightmap tiling and offset: http://unity3d.com/support/documentation/ScriptReference/Renderer-lightmapTilingOffset.html
Create an FBX file from Unity scene. Export both the primary and secondary uv set with the packed UV coordinates. This means that we “offset-scale pack” the per object uv’s we have, into a new “baked uv sheet”. (FBX supports Ascii mode, so it’s quite easy to export)
Launch Max from inside Unity through the commandline batchmode interface, automatically open the exported FBX file and start the lightmapping process
Once the batchmode completes, Unity imports the textures and applies them to the renderers using the Lightmap Settings class and renderer.lightmapIndex.

Here’s a short summary from the discussion with Lucas:

Our main goal is to “unchain” the baking process, so that one can modify the scene in Unity as much as he wants – and in every moment start the bake process (possibly several times during the work over the scene) before, the user were pretty much blocked to do changes in the imported model inside Unity
We’ll test the system with max and vray, but it should work with any fbx reading, lightmap creating program with some additional work
The user would have a choice (by selecting objects from list) which objects are meant to take part in the bake process. On the selection list will be placed combo boxes beside each object, to make user choose a lightmap-enabled shader.
The scene is being exported into ascii-fbx file and then imported into 3dsmax. During the exporting process we set the 3rd channel uv using the existing (second?) channel uv which will be scalled and offseted. (We will demand an unwrap uv on second channel from the user for the beginning – later on it may be created automatically for him) [credits: Joachim Ante]
All the UV’s will be packed to a single or a few big texture sheets – a benefit in performance
We’ve got an idea to make vray materials assigning automatically according to the material name from unity – that would help the designer in preparing the scene to the baking process (when one doesn’t use any keywords in the material name in Unity then the default vrayMtl with a diffuse map (eventually in bump map – if it makes sense) will be assigned.
The light setup in 3dsmax is not yet outvoted – although we’ve got two conceptions:
- The vray-lights are being created dynamically on the image of the lights created in Unity
- We leave the light setup to the 3d artist so he can import a light rig to the scene and then bake
After the baking process is done the materials in Unity stay unchanged, but using the LightmapSettings class the appropriate parts of the lightmap texture are assigned to them (there are a few issues waiting to be resolved)

We’ve also considered some nice icings as for example forwarding 3dsmax communicates and render progress to Unity or a possibility to choose a custom renderer – Mental Ray for instance.

Here is a simple diagram of how the things will work inside

Vray-Unity tools diagram

Filed under: Unity, Vray-Unity tools | 5 Comments

Theory NO. 6 : A point projection matrix to a line (3D)

29Apr09

I was trying to get a matrix for a projection of any point to a line given by the following equotations:

$x=at$
$y=bt$
$z=ct$

After some time of research I’ve ended with the following result:
Let $r=a^2+b^2+c^2$ then
$M= \left ( \begin{matrix} a^2/r & ba/r & ca/r \\ ab/r & b^2/r & cb/r \\ ac/r & bc/r & c^2/r \end{matrix} \right )$

Of course the result isn’t new at all, it was just a big efford for me to do that at midnight – so I guess it may be worth saving it here.

Filed under: Mathematics, Problems, Science, Theory | 1 Comment
Tags: 3d, algebra, line, math, matrix, point, projection

Assembler programming NO. 1

25Apr09

This post is meant to be a short introduction to a new science branch on my blog dedicated programming in Assembler.

One can think that the use of Assembler is deprecated these days, but there are still many reasons for a computer scientist to know this low-level language.

The primary reason to program in assembly language, as opposed to an available high-level language, is that the speed or size of a program is critically important.

For example, consider a computer that controls a piece of machinery, such as a car’s brakes. A computer that is incorporated in another device, such as a car, is called an embedded computer. This type of computer needs to respond rapidly and predictably to events in the outside world. Because a compiler introduces uncertainty about the time cost of operations, programmers may find it difficult to ensure that a high-level language program responds within a definite time interval—say, 1 millisecond after a sensor detects that a tire is skidding. An assembly language programmer, on the other hand, has tight control over which instructions execute. In addition, in embedded applications, reducing a program’s size, so that it fits in fewer memory chips, reduces the cost of the embedded computer.

Here is a picture illustrating the converting process for both high and low level languages.

Source for further reading: http://pages.cs.wisc.edu/~larus/HP_AppA.pdf

Filed under: Assembler, Informatics, Science | 3 Comments
Tags: Assembler, mips, Programming

Theory NO. 5 : Fibbonacci strikes again!

18Feb09

Today, I noticed an amazing and worth memorizing thing. I turns out that fibbonacci series shows up also in graph theory in one of the simplest graphs:

Interesting graph

Where’s Fibbonacci hiden here? Well, the graph can be represented as a folowing matrix:

$M={\left[\begin{array}{ccc} 1 & 1 \\ 1 & 0 \\ \end{array}\right]}$

By multiplying the matrix by itself and using induction we get:

$M^{n} ={\left[\begin{array}{ccc} FIB(n) & FIB(n-1) \\ FIB(n-1) & FIB(n-2) \\ \end{array}\right]}$

Filed under: Mathematics, Science, Theory | 6 Comments

Tweak NO. 3 : Polish characters on Nokia SU-8W

10Feb09

It’s a trick that makes posible to write polish characters on your mobile in Python editor using Nokia SU-8W. All that’s needed is PyS60 installed with appuifw2 module.

To write a polish letter press Alt Gr + Key, where Key is the usual key under which polish character is hiden.

Few things that I could not ommit – the letter “ź” is under key “q” instead of “x” and the capital letter “Ć” is under “W” instead of “C”

Use with the default “UK, US English” layout.

And here’s the pys60 code of the editor:

#Coded by Ranza from Ranza's Research
#published using GNUv3
#https://masteranza.wordpress.com
import key_codes, e32, appuifw2
app_lock=e32.Ao_lock()

def exit():
    app_lock.signal()

appuifw2.app.exit_key_handler=exit

def capt(where,add):
    if (add>0):
        text.move(1, select=True)
        #a
        if (text.get_selection()[2]==u"\u00E1"):
            text.cut()
            text.insert(pos=where,text=u"\u0105")
        #s
        elif (text.get_selection()[2]==u"\u00DF"):
            text.cut()
            text.insert(pos=where,text=u"\u015b")
        #c
        elif (text.get_selection()[2]==u"\u00a9"):
            text.cut()
            text.insert(pos=where,text=u"\u0107")
        #e
        elif (text.get_selection()[2]==u"\u00e9"):
            text.cut()
            text.insert(pos=where,text=u"\u0119")
        #l
        elif (text.get_selection()[2]==u"\u00F8"):
            text.cut()
            text.insert(pos=where,text=u"\u0142")
        #n
        elif (text.get_selection()[2]==u"\u00f1"):
            text.cut()
            text.insert(pos=where,text=u"\u0144")
        #z
        elif (text.get_selection()[2]==u"\u00e6"):
            text.cut()
            text.insert(pos=where,text=u"\u017c")
        #z`
        elif (text.get_selection()[2]==u"\u00e4"):
            text.cut()
            text.insert(pos=where,text=u"\u017a")
        #A
        elif (text.get_selection()[2]==u"\u00c1"):
            text.cut()
            text.insert(pos=where,text=u"\u0104")
        #C, tricky one
        elif (text.get_selection()[2]==u"\u00C5"):
            text.cut()
            text.insert(pos=where,text=u"\u0106")
        #E
        elif (text.get_selection()[2]==u"\u00c9"):
            text.cut()
            text.insert(pos=where,text=u"\u0118")
        #L
        elif (text.get_selection()[2]==u"\u00D8"):
            text.cut()
            text.insert(pos=where,text=u"\u0141")
        #N
        elif (text.get_selection()[2]==u"\u00D1"):
            text.cut()
            text.insert(pos=where,text=u"\u0143")
        #S
        elif (text.get_selection()[2]==u"\u00a7"):
            text.cut()
            text.insert(pos=where,text=u"\u015a")
        #Z
        elif (text.get_selection()[2]==u"\u00c6"):
            text.cut()
            text.insert(pos=where,text=u"\u017b")
        #Z`
        elif (text.get_selection()[2]==u"\u00c4"):
            text.cut()
            text.insert(pos=where,text=u"\u0179")
        text.clear_selection()
        text.move(2)
text=appuifw2.Text(edit_callback=capt)
appuifw2.app.body=text
app_lock.wait()

Well this is not the best solution I’ve invented, but it’s all I could do. I’ve been searching all over internet for hours, trying things to make those characters work everywhere on the phone, but with no success.

Filed under: Informatics, Mobile, Nokia N95, Nokia N95 8GB, Nokia SU-8W, pys60, Python, Tweaks | 2 Comments
Tags: character, layout, polish, pys60, s60, su-8w

Email Subscription

Your email:

Email Address:

Join 42 other subscribers

Top Posts
Archives
- October 2022 (1)
- September 2015 (1)
- May 2015 (1)
- November 2013 (1)
- June 2013 (1)
- June 2012 (1)
- April 2012 (1)
- March 2012 (1)
- January 2010 (2)
- September 2009 (2)
- August 2009 (2)
- July 2009 (2)
- April 2009 (2)
- February 2009 (3)
- January 2009 (1)
- December 2008 (3)
- November 2008 (2)
- September 2008 (2)
- August 2008 (7)
- July 2008 (1)
- June 2008 (4)
- April 2008 (1)
- March 2008 (3)
- February 2008 (3)
- January 2008 (1)
- December 2007 (9)
- November 2007 (3)
- October 2007 (3)
- September 2007 (5)
- August 2007 (3)
I was listening…
- An error has occurred; the feed is probably down. Try again later.
Blog Stats
- 224,554 hits

	dedicated windows se… on Solution: VS C++ 2008 “P…
	dedicated servers ch… on Solution: VS C++ 2008 “P…
	www.escinf.Una.Ac.cr on Solution: VS C++ 2008 “P…
	파친코 on OSX Productivity Tip NO.1
	텍사스홀덤 on OSX Productivity Tip NO.1